1. 벡터
벡터는 샘플을 n차원의 특징 벡터로 표현합니다. 예로 들어서 데이터에서 꽃받침의 길이, 너비, 꽃잎의 길이, 너비는 4가지 특징이기 때문에 4차원의 특징 벡터로 표현하게 됩니다.
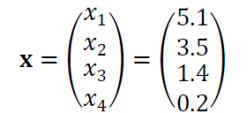
여러 개의 특징 벡터가 존재한다면, 이는 첨자로 구분하게 됩니다.
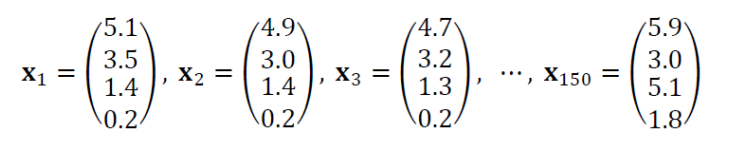
다음은 행렬입니다. 만약 여러 개의 벡터가 쌓인다면, 이는 행렬로도 표현할 수 있습니다. 예로 들어 붓꽃 데이터가 있는 150개의 샘플이 있따고 하면, 이는 다음과 표현할 수 있습니다.

이러한 행렬도 쌓이면 3차원 이상으로 표현할 수 있습니다. 이를 텐서라고 합니다. 이 텐서는 보통 RGB 컬러 영상들이 쌓이는 경우 이를 표현하기 위한 도구로도 사용됩니다.

지금까지는 데이터를 표현하기 위한 방법에 대해 서술해보았습니다. 이제 벡터와 행렬의 크기를 측정하는 방법에 대해 알아보겠습니다. 벡터에는 p차 놈이라는 것을 적용할 수 있습니다. 벡터 안에 있는 행을 전부 p차 제곱해서 더한 뒤 이 전체 합값을 1/p 제곱을 해주는 것입니다.

그리고 이 중 제일 최대의 놈이란 것을 정할 수도 있는데, 이는 벡터안에 있는 값들을 전부 절대값을 구해 그 중 가장 큰 것을 구하는 것을 말합니다. 예로 들어 4, 8, -10, 3이 벡터 안에 있다면 최대 놈은 10이겠죠?
행렬의 경우는 프로베니우스 놈이란 물건을 이용해서, 크기를 측정합니다. 이 방식은 모든 값을 더해서 이를 1/2제곱(루트 제곱)을 해주는 방식입니다.

다음은 이제 수식으로 표현했던 특징 벡터를 기하학적으로 표현해보자.

벡터는 화살표를 이용해서 다음과 같이 표현할 수 있다. 그리고 데이터간의 유사도는 각도를 많이 이용하기 때문에 cosine을 이용해서 많이 표현하는 편입니다.

이제, 선형대수는 많이 보았으니, 퍼셉트론 이야기 좀 하겠습니다. 퍼셉트론은 사람의 뇌의 능력을 시뮬레이션하고, 표현하기 위해 만들어진 컴퓨터의 모델이나 기계를 의미합니다. 즉 사람처럼 물체를 인식하고 구별하는 그런 것을 하기 위한 능력을 기계를 의미합니다.

굉장히 간단한 구조를 가지고 있습니다. weight function, summation, threshold operator로 구성됩니다. 입력이 들어오면 각 입력에 weight를 곱해준 뒤 weight된 값들을 더해준 뒤 threshold된 값에 맞춰서 반환을 합니다. 이 때 활성함수란 것을 이용해서 반환을 하게 됩니다.

그리고 이러한 weight 직선을 법선 벡터를 표현하면 다음과 같이 표현됩니다.
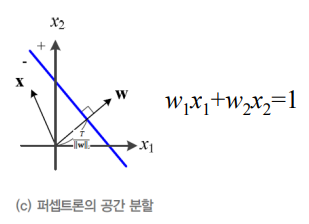
그리고 이러한 퍼셉트론의 동작을 수식으로 표현하면 다음과 같습니다.

그럼 2차원 말고 3차원 이상의 경우는 어떻게 표현할까? 다음과 같은 3차원 벡터가 입력으로 들어갔다고 가정하자.

이 때 2차원은 결정 직선을 이용해서 분류를 했다면, 3차원 공간에서는 결정 평면을 이용하며, W에 수직이고 T/|w|2만큼 떨어져 있다고 볼 수 있다.

만약 출력이 여러개라면 다음과 같이 표기한다.
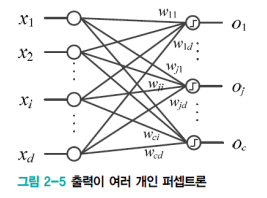

그리고 j번째 퍼셉트론의 가중치 벡터는 다음과 같이 표현한다.

이제 이러한 동작을 수식으로 표현하면 다음과 같다.

이러한 output이 있다고 하자. 그럼 이 때 W가 다음과 같으면

이제 이를 행렬로 간단하게 쓰면 다음과 같이 표현한다.

즉 가중치 벡터를 각 부류의 기준 벡터로 가정한다면, c개의 부류의 유사도를 계산하는 것과 같은 이치인 것이다.
자 이제 이러한 퍼셉트론을 통해서 학습에 대해 정의를 해보자. 학습을 마친 프로그램을 현장에 설치했을 경우 일어나는 과정은 식으로 표현하면 다음과 같다.

그리고 학습은 훈련 집합의 샘플에 대해 다음 식처럼 가장 잘 만족하는 W를 찾아내는 과정이라 볼 수 있다.

즉 분류를 위한 과업은 이미 W는 정해져있고, 입력 값이 주어지면 이에 대한 x가 주어지는 과정이며, 학습은 입력값과, 출력값은 이미 정해져있으며, 이 과정에서 W를 유추하는 과정이라 볼 수 있다.
즉 현대의 기계학습에서 퍼셉트론은 여러 층을 확장해서 만드는 과정인데, 이 과정에서 W가 정해진다고 보면 된다.
이제 학습에 대한 이야기를 했으니, 다시 정부호와, 고유벡터, 고유 행렬을 구하는 것에 대해서 서술해보겠다. 일단 정부호가 무엇인가 하면 특정 조건에 따라서 행렬이 양수나 음수로 표현되는 것을 말합니다. 즉 0이 아닌 모든 벡터에 대해, 행렬 A가 0보다 큰가 작은가를 판별하는 것을 말합니다.


이제 행렬을 분해를 해보도록 하겠습니다. 어떤 행렬에 고유벡터 v를 곱한 값은 고윳값 람다에 v를 곱한 값과 같은 것읍니다. 예로 들어 아래와 같은 행렬과 벡터가 있다고 가정합시다.


이에 대한 람다는 다음과 같이 표현할 수 있습니다.

이제 행렬로부터 고윳값을 분해하기 위해서는 다음과 같은 과정을 거칩니다.

이 때 Q는 A의 고유 벡터를 열에 배치한 행렬이며, A 비슷하게 생긴 저 행렬은 고윳값을 대각선으로 배치한 대각행렬입니다. 그래서 예로들면 다음과 같습니다.

이러한 분래의 과정은 오로지 정사각행렬에만 적용이 가능합니다. 하지만 경우에 따라서는 정방행렬이 아닌 경우가 있을 것입니다. 즉 이러한 한계를 가지기 때문에 나온 것이 바로 특잇값 분해라는 수식입니다. 이 특잇값 분해는 n*m 즉 정방행렬이 아니더라도 적용이 가능합니다. 수식은 다음과 같습니다.

먼저 U는 n*n행렬을 가집니다. 그리고 V행렬은 m*m을 가집니다. 그럼 당연히 시그마 행렬의 크기는 n*m이겠죠? 예로 들어 4*3 행렬이 있다면 다음과 같이 연산을 진행합니다.

이렇게 구한 고유값은 타원의 장단축 길이를 결정하고, 고유벡터는 방향을 결정을 합니다.
'Deep Learning' 카테고리의 다른 글
| [딥러닝] 최적화 이론 (0) | 2021.10.17 |
|---|---|
| [딥러닝, 수학] 확률과 통계 (0) | 2021.10.17 |
| [딥러닝] 간단한 기계학습 (0) | 2021.10.12 |
| [딥러닝] 인공지능과 데이터 (0) | 2021.10.12 |
| [인공지능] 특징 공간 (0) | 2021.10.12 |



