우리는 어떤 화면을 통해 컴퓨터가 그려내는 이미지 세상을 본다. 즉 화면에는 이 화면에 맞는 내용만 출력이 되어야한다는 뜻이며, 이 외의 나머지 물체나 배경은 출력이 되선 안 된다. 이 것을 바로 Window clipping이라고 한다.
어떠한 Min(Xmin, Ymin)부터 Max(Xmax, Ymax)까지로 한정된 Window 내부에 있는 부분만 잘라서 그리는데 과연 어떤 알고리즘이 필요한 지 알아보자.
1. Line Clipping (라인 클리핑)
예로들어 선분이 윈도우에 다음과 같이 걸쳐있다고 가정하자.
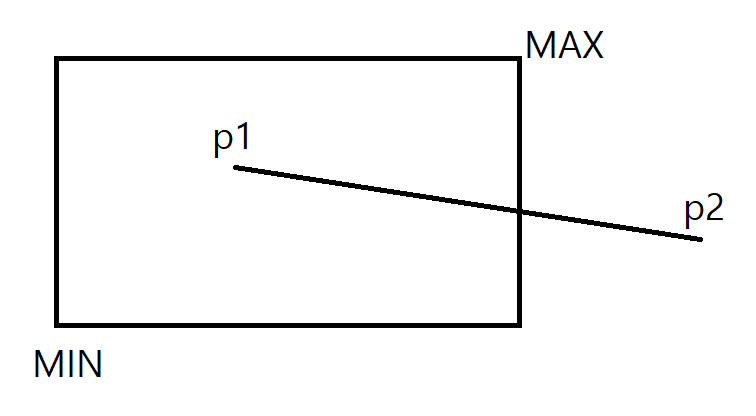
이 때 두 점 p1(x1, y1)과 p2(x2, y2)를 잇는 선분의 w의 내부만을 어떻게 그릴 것인가.
여기서는 보통 2가지 알고리즘이 사용된다.
1. Cohen-sutherland 알고리즘
일단 아래처럼 윈도우 포함 주변을 9개의 영역으로 구별한다.

그리고 각 영역별로 4비트 코드를 두어 구별한다. 코드는 다음 순으로 주어진다. Left-Right-Top-Bottom
즉 만약 1010이면 맨 위의 왼쪽이란 뜻이다. 이를 뒤 사진으로 다시 정리하면 다음과 같아진다.
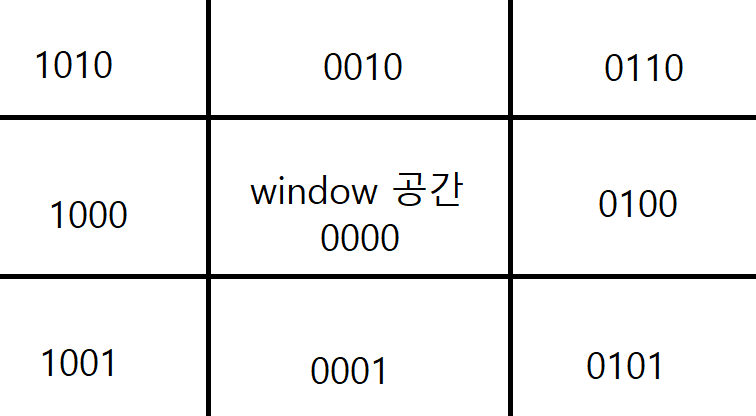
이제 전처리 작업은 완료되었다. 이제 p1과 p2의 area code를 파악할 필요가 있다.
이 때 주의해야할 것은 1000구간에서 0000 즉 window 공간을 통과해서 0100인 경우. 또는 둘 다 0000을 지나가지 않는 경우를 다 구별을 해야한다.
Algorithm
{
c1 = area code of p1;
c2 = area code of p2;
// 둘 다 Window 공간을 지나가지 않는 경우
// (즉 한 쪽에 치우쳐져서 and 연산자로 0000이 아닌 경우)
if(c1 & c2 != 0000) full reject;
// 둘 다 Window 공간 내에 있는 경우
// 즉 둘 다 Window 공간 내에 있는 경우
if(c1 | c2 == 0000) full accept;
// Actual Clipping (4 edge를 따라서 한 번에 clipping)
}
위의 Actual clipping 부분에서 일어나는 작업을 그림으로 그리면 다음과 같다.

이 알고리즘의 특징은 Window의 경계에 걸치지 않은 선분들이 많을 때 유리하다고 볼 수 있다. 왜냐면 경계에 걸친다면 결국은 if문으로 처리가 되지 않고 이에 대한 Actual 연산이 진행이 되며 이러한 선분들이 많아지면 결국 성능을 많이 잡아먹기 때문이다.
그럼 만약 이렇게 잘라내야 될 선분이 많은 경우에 어떻게 해야할 까에 대해 고민이 들 것이다. 이러한 경우를 위해 존재하는 것이 바로 아래서 소개할 알고리즘이다.
2. Liang-Barsky 알고리즘
이 알고리즘도 결국 Window의 4변을 따라서 Clipping을 해야하는 것은 똑같기 때문에 Area code같은 걸 생각하지 않고 바로 Clipping으로 들어간다.
일단 선분을 매개변수 방정식으로 표현한다. 그러면 p1, p2가 나올 것이다. 그럼 매개변수 방정식으로 표현한다는 말이 무엇인지 설명하겠다.
일단 p1, p2가 같은 선에 있다 가정하고 이 선분 위에 임의의 점 p가 있다고 가정하자. 즉 p1, p2는 vector v를 만들 수 있으며, 이 방향 vector와 평행할 것이다.

과연 이 방정식이 직선의 방정식으로 맞는 지에 대해 고려해야 한다면 t에 0과 1을 넣어본다. 만약 0을 넣었는데 p1이 나오며 1을 넣었을 때 p2가 나온다면 이 방정식은 타당한 것이다. 즉 다음과 같이 정리할 수 있다.

이제 Clipping에 쓸 벡터 방정식이 정리가 되었다. (t가 0~1 사이라면 그 선분을 나타낸다.) 이제 이 것을 이용해서 직접 잘라내는 것은 아래의 부등식을 푸는 것이다.

이 떄 모든 것은 상수지만 t만 변수이다.

즉 이를 그림으로 표현하면 다음과 같다.
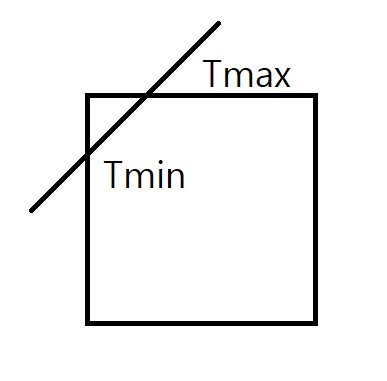
이 알고리즘의 특징은 위에서 말한대로 만약 Window에 걸친 선분들이 많을 떄 유리한 방식이다.
'Graphics' 카테고리의 다른 글
| [Graphics] 05. 3차원상 물체 변환 (0) | 2021.12.21 |
|---|---|
| [Graphics] 04. 2차원상 물체 변환 (0) | 2021.12.21 |
| [Graphics] 02. 디스플레이와 그리기 방정식 (0) | 2021.12.21 |
| [Graphics] 01. 컴퓨터 그래픽스의 중심. 영상과 색 (0) | 2021.12.21 |
| [Graphics] 쉐이더란 무엇인가 (0) | 2021.12.21 |



